Schématisation cinématique

Introduction

Notion de Mécanisme et de Solides

Définition :

On appelle mécanisme, un ensemble de pièces mécaniques reliées entre elles par des liaisons, en vue de réaliser une fonction déterminée.

Nous admettrons que les pièces mécaniques peuvent être modélisées par des solides indéformables.

Exception : les pièces dont la fonction est de se déformer (ressorts, joints, etc...)

Fondamental : Solide indéformable

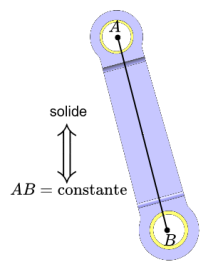
Le solide indéformable possède une masse constante et un volume dont les limites sont invariantes quelles que soient les actions extérieures auxquelles il est soumis.

Exemple : la bielle du micromoteur est supposée indéformable ↔ la distance entre ses points A et B est constante .

Paramétrage de la position d’un solide

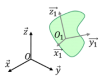
Pour connaitre la position de tous ses points dans l’espace, il suffit de connaitre la position d’un repère lié à ce solide.

Notons $Équation en notation Latex : R\left(O,\vec{x},\vec{y},\vec{z}\right)$ le repère de référence et $Équation en notation Latex : R\left(O_1,\vec{x_1},\vec{y_1},\vec{z_1}\right)$ le repère lié au solide.

La position du solide dans l’espace, est déterminée par 6 paramètres indépendants :

Position du point O₁ dans R : 3 coordonnées
Orientation de 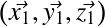$Équation en notation Latex : \left(\vec{x_1},\vec{y_1},\vec{z_1}\right)$ par rapport à 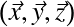$Équation en notation Latex : \left(\vec{x},\vec{y},\vec{z}\right)$ : 3 angles

Fondamental : Degré de liberté d’un solide

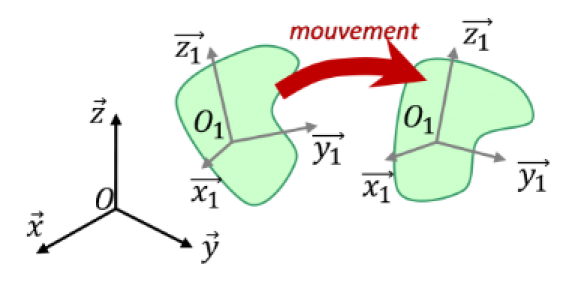
On appelle « libertés » d’un solide par rapport à un référentiel, les mouvements indépendants de ce solide pour passer d’une position à une autre.

Il existe deux mouvements élémentaires entre les solides :

Le mouvement de TRANSLATION (RECTILIGNE) : les trajectoires de tous les points du solide sont des droites parallèles.

Le mouvement de ROTATION : les trajectoires de chaque point sont des cercles coaxiaux.

ATTENTION : Pour définir un mouvement, il est nécessaire de fixer une référence. La notion de mouvement est toujours relative : c’est le mouvement d’un système par rapport à un référentiel (ici défini par le repère R).

On dit que le solide possède des degrés de liberté, chacun contrôlés par :

Soit un paramètre de position linéaire = translation

Soit un paramètre de position angulaire = rotation

Exemple :

Par exemple, dans un repère $Équation en notation Latex : R\left(O,\vec{x},\vec{y},\vec{z}\right)$ , on pourra les noter :

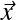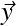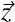
Tx, Ty et Tz pour translations selon les axes $Équation en notation Latex : \vec{x}$ , $Équation en notation Latex : \vec{y}$ et $Équation en notation Latex : \vec{z}$
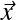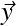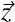
Rx, Ry et Rz pour rotations autour des axes $Équation en notation Latex : \vec{x}$ , $Équation en notation Latex : \vec{y}$ et $Équation en notation Latex : \vec{z}$

Remarque :

Un solide possède au maximum 6 degrés de liberté et au minimum 0.

Le schéma cinématique, à quoi ça sert ?

Définition :

Par définition, un mécanisme est composé de plusieurs sous ensembles reliés entre eux par une ou plusieurs liaisons.

Mais la lecture des plans d'ensemble n'est pas toujours aisée et il est utile d'en simplifier la représentation.
Lorsque le mécanisme n'existe pas (phase de conception), on a besoin d'un schéma illustrant le fonctionnement attendu sans toutefois limiter le concepteur dans les formes et dimensions à concevoir.

Que faut-il donc représenter ?

Le schéma cinématique doit représenter le plus fidèlement et le plus simplement possible les relations entre les différents groupes de pièces.

On trouvera donc :

Des groupes de pièces représentés sous forme de « fils de fer ». On les appelle aussi « blocs cinématiques » ou aussi « classes d'équivalence ».

Des liaisons normalisées situées au niveau de chaque contact entre les groupes de pièces.

Des exemples…

Exemple : Le serre-joint

Exemple : Un étau

Mais comment fait-on tout ça ?

Les liaisons normalisées

Introduction

Avant de détailler la méthode, voyons d'abord quelles sont les liaisons normalisées, comment on les distingue et comment elles sont représentées.

Il y en a 11 au total.

La Liaison encastrement

Fondamental :

Nom de la liaison	Degrés de liberté	Mouvements relatifs		Représentation normalisée
Nom de la liaison	Degrés de liberté	Mouvements relatifs		Vues planes	Perspective
Encastrement	0	0	Translation(s)
Encastrement	0	0	Rotation(s)

Simulation :

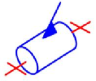
La liaison pivot

Fondamental :

Nom de la liaison	Degrés de liberté	Mouvements relatifs		Représentation normalisée
Nom de la liaison	Degrés de liberté	Mouvements relatifs		Vues planes	Perspective
Pivot	1	0	Translation(s)
Pivot	1	1	Rotation(s)

Simulation :

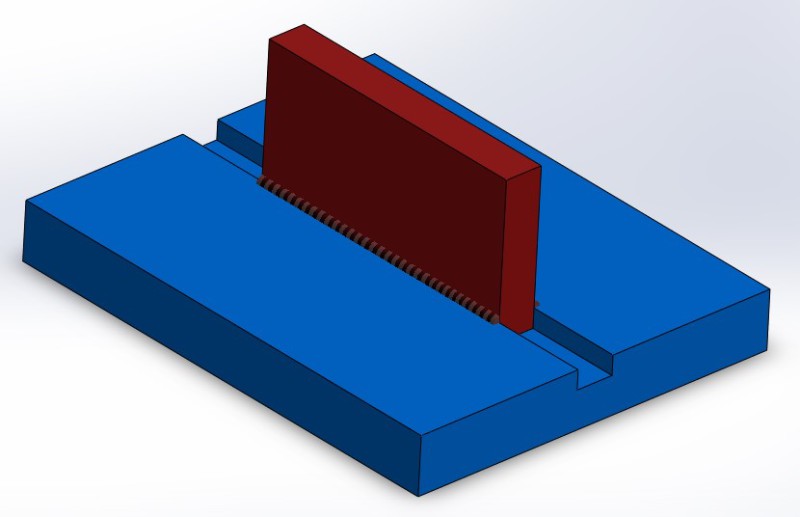
La liaison glissière

Fondamental :

Nom de la liaison	Degrés de liberté	Mouvements relatifs		Représentation normalisée
Nom de la liaison	Degrés de liberté	Mouvements relatifs		Vues planes	Perspective
Glissière	1	1	Translation(s)
Glissière	1	0	Rotation(s)

Simulation :

La liaison hélicoïdale

Fondamental :

Nom de la liaison	Degrés de liberté	Mouvements relatifs		Représentation normalisée
Nom de la liaison	Degrés de liberté	Mouvements relatifs		Vues planes	Perspective
Hélicoïdale	1	1	Translation(s)
Hélicoïdale	1	1	Rotation(s)

Remarque :

La liaison hélicoïdale ne permet qu'un seul degré de liberté puisque les 2 mouvements relatifs ne sont pas indépendants.

On dit qu'ils sont conjugués.

Simulation :

Le pivot glissant

Fondamental :

Nom de la liaison	Degrés de liberté	Mouvements relatifs		Représentation normalisée
Nom de la liaison	Degrés de liberté	Mouvements relatifs		Vues planes	Perspective
Pivot glissant	2	1	Translation(s)
Pivot glissant	2	1	Rotation(s)

Simulation :

La liaison sphérique à doigt

Fondamental :

Nom de la liaison	Degrés de liberté	Mouvements relatifs		Représentation normalisée
Nom de la liaison	Degrés de liberté	Mouvements relatifs		Vues planes	Perspective
Sphérique à doigt	2	0	Translation(s)
Sphérique à doigt	2	2	Rotation(s)

Simulation :

La liaison appui plan

Fondamental :

Nom de la liaison	Degrés de liberté	Mouvements relatifs		Représentation normalisée
Nom de la liaison	Degrés de liberté	Mouvements relatifs		Vues planes	Perspective
Appui plan	3	2	Translation(s)
Appui plan	3	1	Rotation(s)

Simulation :

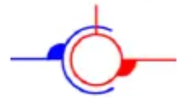
La liaison rotule

Fondamental :

Nom de la liaison	Degrés de liberté	Mouvements relatifs		Représentation normalisée
Nom de la liaison	Degrés de liberté	Mouvements relatifs		Vues planes	Perspective
Rotule	3	0	Translation(s)
Rotule	3	3	Rotation(s)

Simulation :

La liaison linéaire annulaire

Fondamental :

Nom de la liaison	Degrés de liberté	Mouvements relatifs		Représentation normalisée
Nom de la liaison	Degrés de liberté	Mouvements relatifs		Vues planes	Perspective
Linéaire annulaire	4	1	Translation(s)
Linéaire annulaire	4	3	Rotation(s)

Simulation :

La liaison linéaire rectiligne

Fondamental :

Nom de la liaison	Degrés de liberté	Mouvements relatifs		Représentation normalisée
Nom de la liaison	Degrés de liberté	Mouvements relatifs		Vues planes	Perspective
Linéaire rectiligne	4	2	Translation(s)
Linéaire rectiligne	4	2	Rotation(s)

Simulation :

La liaison ponctuelle

Fondamental :

Nom de la liaison	Degrés de liberté	Mouvements relatifs		Représentation normalisée
Nom de la liaison	Degrés de liberté	Mouvements relatifs		Vues planes	Perspective
Ponctuelle	5	2	Translation(s)	ou
Ponctuelle	5	3	Rotation(s)	ou

Simulation :

Méthode d'élaboration

Les étapes

Méthode : Étape 1 : Repérer les groupes cinématiques

Colorier les classes d'équivalences sur le plan d'ensemble.
Recenser les pièces composant chaque groupe. (les pièces élastiques à exclure)

Méthode : Étape 2 : Établir le graphe des liaisons

Relier par un trait les groupes ayant des contacts quels qu’ils soient.

Méthode : Étape 3 : Identifier les liaisons entre les groupes

Déterminer la nature du ou des contacts entre les classes d’équivalence.
Et/Ou observer les degrés de liberté entre les groupes concernés.
En déduire la liaison normalisée correspondante (centre et axe).

Méthode : Étape 4 : Construire le schéma cinématique minimal

Choisir un point de vue de représentation (plan).
Repérer la position relative des liaisons (au centre du contact réel).
Placer les liaisons sur les points identifiés précédemment.
Relier les liaisons entre elles en respectant les blocs (couleurs).
Terminer l’habillage du schéma.

Exemple

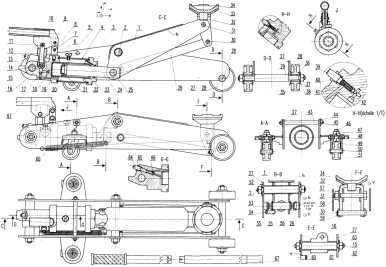
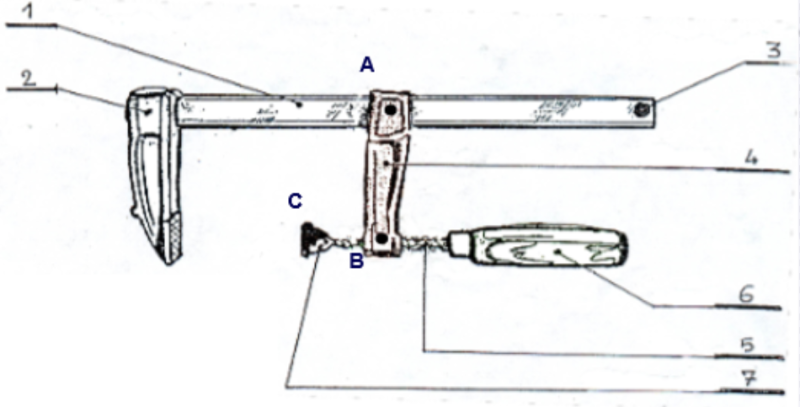
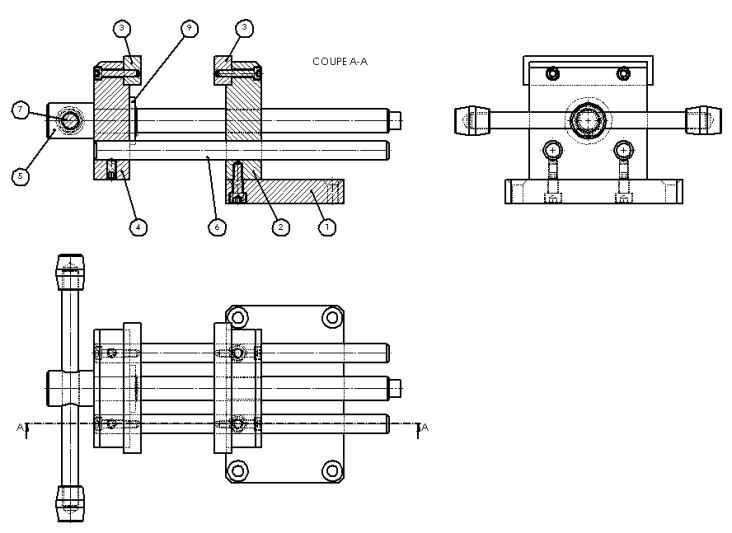
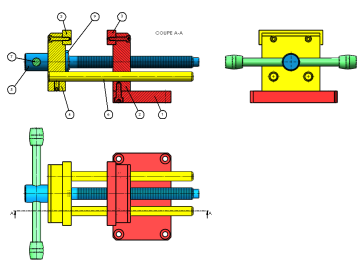
Exemple : Schéma cinématique d'un étau

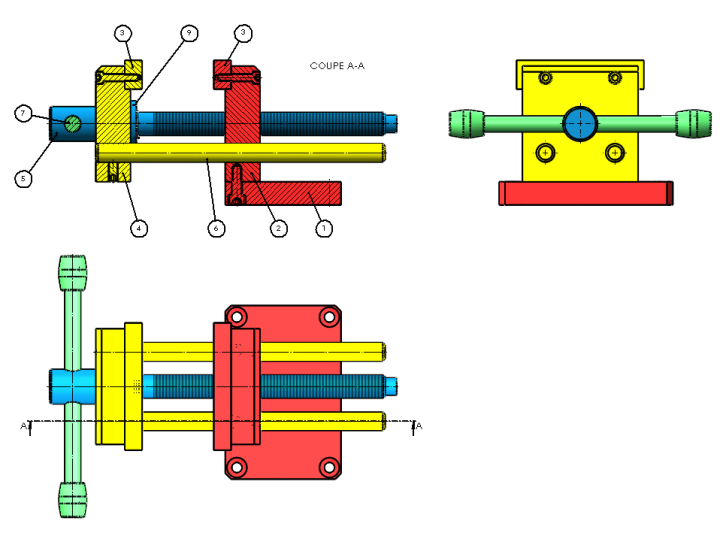
Simulation : Étape 1 : Repérer les groupes cinématiques

Ce repérage s’effectue en observant le plan d’ensemble ou le mécanisme lui-même s’il est à notre disposition. Sur le plan, la meilleure méthode consiste à colorier d’une même couleur les groupes de pièces en liaison encastrement.

Recenser les pièces de chaque groupe.

Groupe 1 : 1 ; 2 ; 3 5 (en rouge)

Groupe 2 : 3' ; 4 ; 6 (en jaune)

Groupe 3 : 5 ; 9 (en bleu)

Groupe 4 : 7 (en vert)

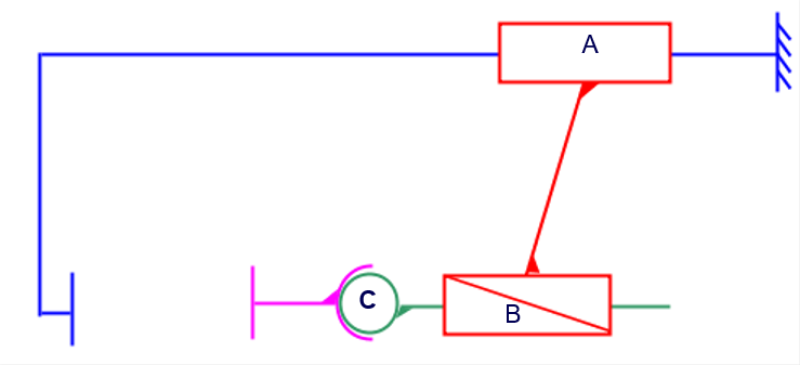
Simulation : Étape 2 : Établir le graphe des liaisons

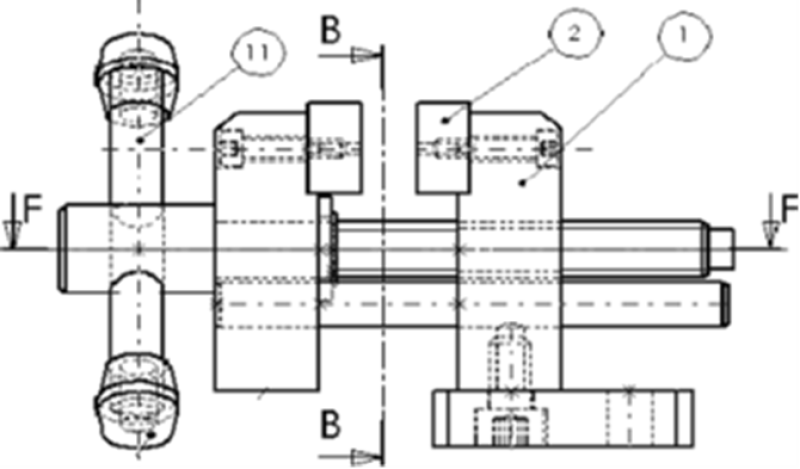
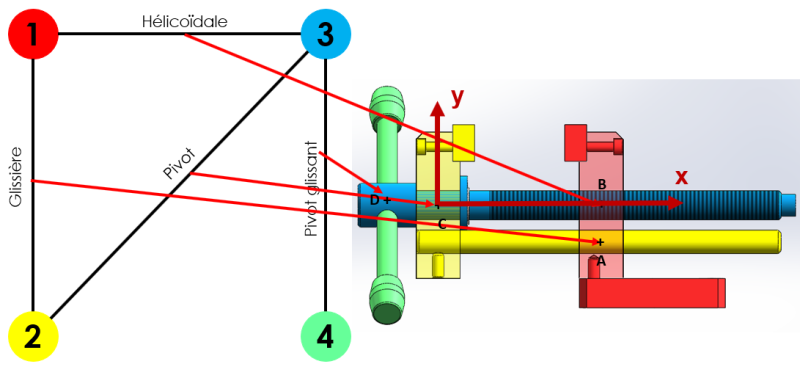
Le graphe des liaisons a pour but d’établir les relations existant entre les groupes identifiés précédemment. On va donc, de manière systématique observer les contacts éventuels entre groupes.

Zoom	Relier par un trait les groupes ayant des contacts quels qu’ils soient.

Simulation : Étape 3 : Identifier les liaisons entre les groupes

Déterminer la nature du ou des contacts entre les groupes et/ou observer les degrés de liberté entre les groupes concernés.

En déduire la liaison normalisée correspondante (centre et axe).

(Cliquer sur l'image ci-dessous pour faire avancer l'animation)

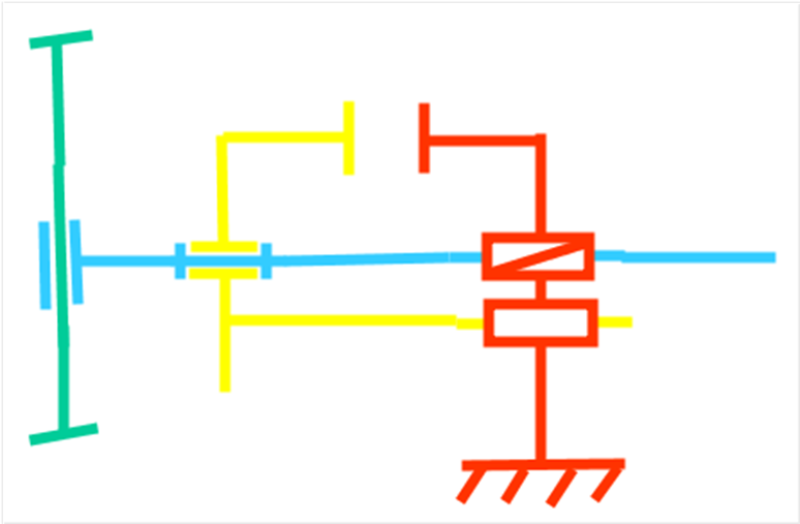
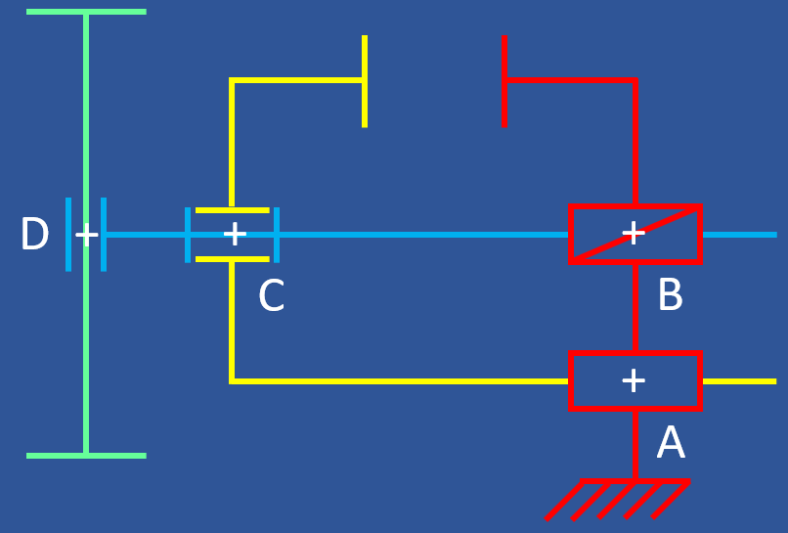
Simulation : Étape 4 : Construire le schéma cinématique

Choisir le point de vue le plus explicite pour le schéma (plan x,y).
Repérer la position relative des liaisons (au centre du contact réel)

Maintenant, vous n'avez plus besoin du plan…

Placer les liaisons sur les points identifiés précédemment.
Relier les liaisons entre elles en respectant les blocs (couleurs).
Terminer l'habillage du schéma.

Votre schéma est terminé !

Compléments…

Modélisation des roulements

Principe

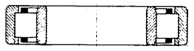
En fonction des indications de comportement fournies par les constructeurs, nous proposons de modéliser la liaison entre bague intérieure et bague extérieure des différents roulements de la manière suivante :

Type de roulement			Modélisation
Désignation	Vue plan	Illustration	Modélisation
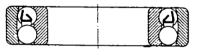
À billes			Rotule
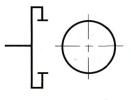
À deux rangées de billes			Pivot
À rouleaux cylindriques			Linéaire annulaire
À aiguilles			Pivot glissant
À rotule			Rotule
À rouleaux coniques			Rotule
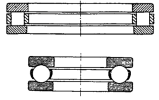
Butée à billes ou à rouleaux			Appui plan

Modélisation des engrenages

Schématisations

La normalisation indiquée ci-dessous permet de représenter schématiquement les engrenages et les chaînes cinématiques usuelles.

Schémas cinématiques (normalisation)


roue extérieure	roue intérieure	roue conique	roue et crémaillère

denture extérieure	denture intérieure

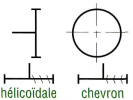
engrenages droits		engrenages coniques	roue et vis sans fin